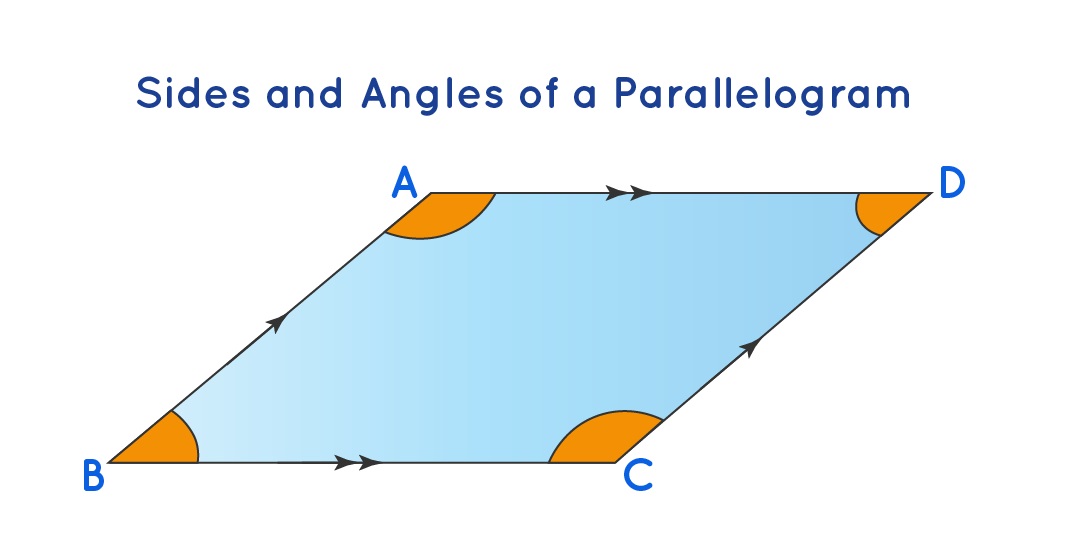
The parallelogram is just a type of polygon and it can also be considered as a quadrilateral that will have the opposite sides which are parallel to each other. To determine if the quadrilateral is having properties of parallelogram or not it is very much important for the students to be clear about different kinds of properties associated with the whole process.
Important properties of parallelogram which are must be understood by every student:
- The opposite sides are parallel: Parallel lines will be the ones that are always at the same distance apart and never touch each other and if the sides of the parallelogram are based upon these lines then opposite sides will never touch each other which will make sure that they will be always at the same distance away from each other no matter how far they can be extended. So, if a particular quadrilateral has two opposite sides which are parallel then it can be considered as a parallelogram.
- The opposite sides will be congruent: The term congruent means two things that are very much identical to each other and if it has been superimposed on the other one then there will be no issue and there will be an exact match. The parallelogram will help in satisfying this particular property because each of the opposite sides will be the same in terms of length and even if the individuals try to break the shape apart and place them on top of each other they will superimpose perfectly which will make sure that opposite sides will be congruent.
- Opposite angles are congruent: Similarly, as the sides are congruent the angles of the parallelogram will also be congruent and the angles will be congruent if they will have the same measure. So, if the students measure the angles of a parallelogram which are opposite with the help of a protractor then they will find out that both of them will be of equal measure and hence they will be congruent because they have the same measurement in the protractor.
- Consecutive angles will be supplementary: To find out that a particular quadrilateral is a parallelogram or not it is very much important for the students to ensure that they take into consideration the consecutive angles. Supplementary angles will be the ones that add up to 180° and two consecutive angles into a parallelogram will be supplementary which is another very important property of this particular type of quadrilateral.
- Diagonals will bisect each other: It is very much important for the students to draw the imaginary line from one angle to the opposite congruent angle and this particular line should create two congruent triangles within this particular shape. From there the individuals need to proceed to draw the other imaginary figure from the supplementary angle to the opposite congruent angle and when these two lines will bisect each other it will divide the parallelogram into two exactly equal parts. Hence, the diagonals of the parallelogram will bisect each other and this particular point has been proved with the help of the above-mentioned explanation.
- If one angle is a right angle: The last property of the parallelogram is that if one angle in the quadrilateral is a right angle then the rest of the angles will also be right angles because the executive angles are supplementary property and the next executive will also come out to be 90° because the sum has to be 180°. Hence, if the one angle of the parallelogram will be 90° then it will be considered as a rectangle rather than a normal parallelogram.
Hence, to be aware of all these kinds of properties of parallelogram the parents need to enrol their students on platforms like Cuemath because the experts over there will help in providing students with clear-cut doubt clearing sessions about the parallelogram so that they never face any kind of issues and unable to perform very well into the examinations.